Subroutines part 2
We have a problem when we have a chain of subroutine calls that is more than one level deep.
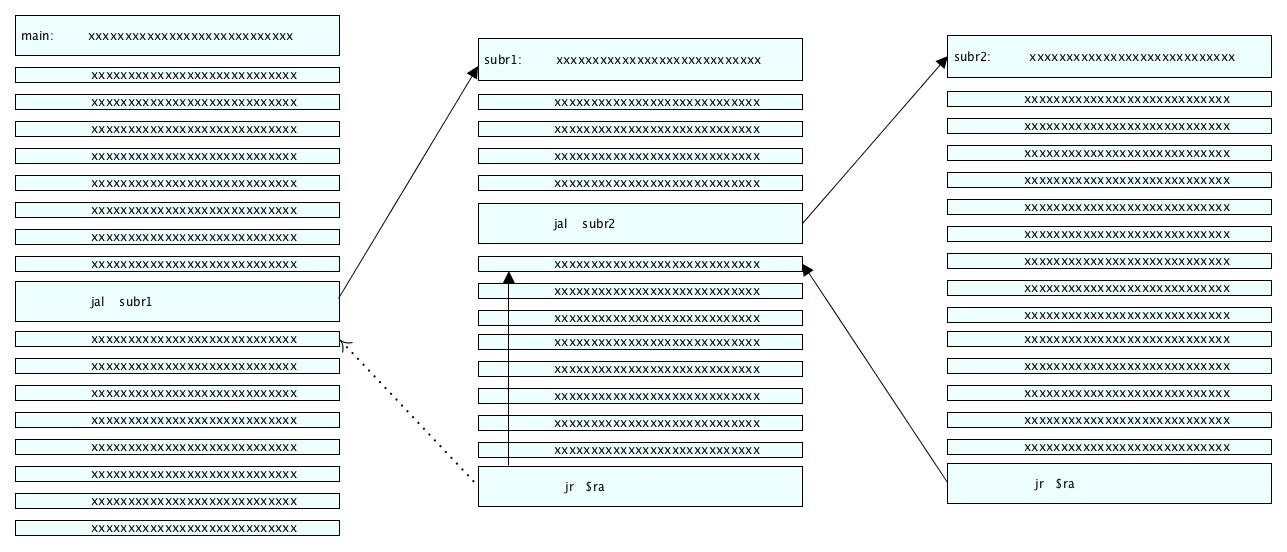
In the picture below main calls subr1, and subr1 calls subr2.
The problem occurs when subr1 trys to return to main.
Register $ra still holds the return address in subr1.
This means that, instead of following the dotted arrow as we intended,
the jr will follow the solid arrow that leads back into subr1.
In fact, we have an infinite loop here.
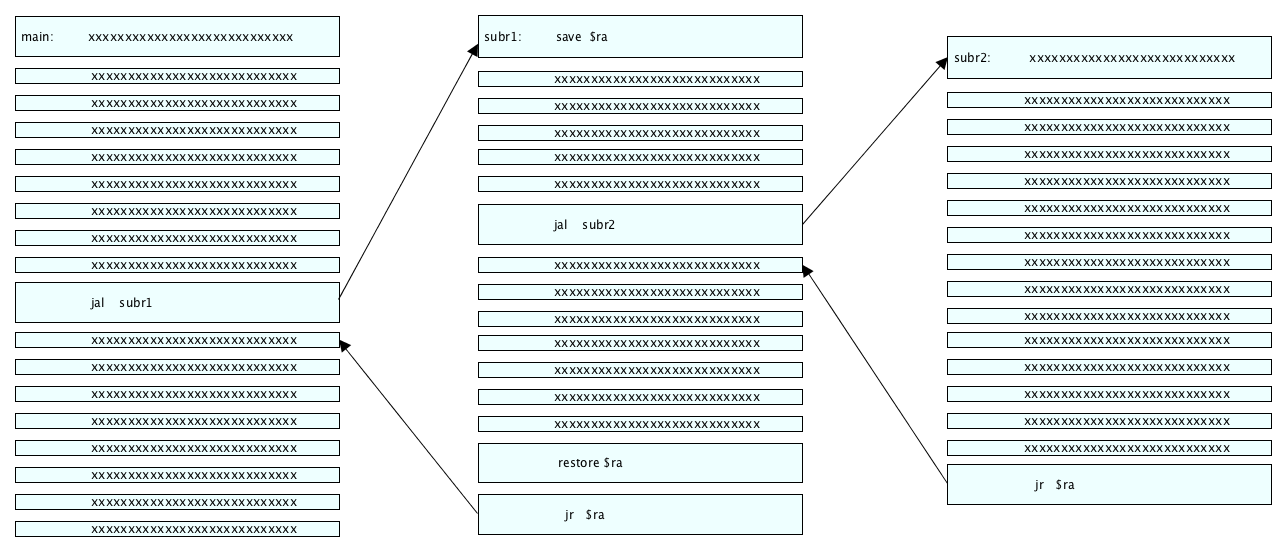
What we need is a mechanism that corrects the value in $ra just before we need it
in the jr instruction at the end of subr1.
This mechanism saves $ra in a special hidey hole
at the beginning of subr1 and then restores it at the end.
In between we can call as many subroutines as we like.
This brings up the question of where this hidey hole can be.
We obviously need more than one of them since we could have main --> subr1 --> subr2 --> subr3.
In this case both subr2 and subr3 would need to save and restore their $ra's.
In fact, this nesting of subroutine calls can be arbitrarily deep, limited only by hardware resources.
We obviously don't have enough registers for this.
The only place we have with enough room is memory.
This leaves us with the question of how can we organize these hidey holes in memory.
Observe that, when we have a nested chain of subroutine calls, they will return in reverse order.
Therefore, what we need is a stack, i.e. last in first out.
If we go back to our example on this page, subr1 will push its return address onto the stack first,
and then subr2 will push its on next.
When subr2 is ready to return, it will pop the stack, and, sure enough, it gets its own return address back.
Then subr1 will pop the stack and get its return address back.
In fact, a stack is the perfect data structure for any sequence of calls and returns, no matter how complex.
In practice, main also saves and restores its return address since it is called as a subroutine by the OS.
Here is a diagram known as a call tree. A calls B, and B calls C.
Next C returns, and B calls D, which then calls E. E, D, and B then return.
A calls F, which calls G. Finally G and F return, and that is the end of the calls.
C, E, and G are known as leaf subroutines. They don't call any others.
Let's think about how the stack will look at various times:
- while C is active, the stack has B on top with A underneath it
- while E is active, the stack, from top to bottom, contains D, B, and A
- while G is active, the stack has F on top with A underneath it
- while D is active, the stack has B on top with A underneath it
The bottom line is that the stack is quite dynamic, growing and shrinking often.
Those who went before us found a clever way to implement a stack in memory that does not require
items in the stack to move as new items come and go above them: the bottom of the stack is fixed,
and the top moves.
Look at the figure on page A-21 in the book. It has a high-level view of memory with no details.
Only the locations of the large memory areas are shown: the text segment, the data segment,
and the stack segment. While you're there, check out the starting addresses of these segments.
The text segment starts at our well-known magic number 0x00400000.
The data segment, however starts at 0x10000000, not 0x10010000.
I think that this means that the MARS guys decided to leave some empty space at the bottom of
the data segment just in case the text segment were somehow to grow upward out of its own area.
Notice that the stack segment is rooted at the top of memory and grows downward.
So, get used to it, the stack is upside down;
its top is in the lowest memory address currently in use by the stack.
Pushing an item onto the top of the stack means adding a new location just below all the others.
Since the top of the stack is constantly moving, we need a way to keep up with where it is.
Register $29 is named $sp; it is the stack pointer
and always holds the address of the top of the stack.
We add an item to the top of the stack by decrementing the stack pointer
and using it in register-indirect mode to address the new stack location.
We remove the top item from the stack by incrementing the stack pointer.