Related Bases 1
We don't care at all about base 100, but we start here because you are familiar with
base 10, so the arithmetic is easy, and the result is pretty obvious anyway.
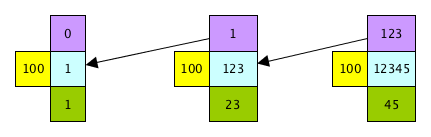
Let's convert 12345 decimal to base 100.
- start at the right side of the page
- divisor (always 100 in this case) is yellow; dividend is aqua; quotient is purple; remainder is green
- divide the original numeral (12345) by the new base (100), which gives you a quotient (123) and a remainder (45)
- long division procedure guarantees that the remainder will be less than the divisor (100 in this case)
- now repeat until the quotient is zero
- move to the left
- write down the quotient from the last division (arrows)
- make it a new division problem using the same divisor
- do the division, getting another quotient and remainder
- the answer is the string of remainders read left to right (1, 23, 45 in this case)
- I hope that you find it obvious that we didn't need to do the division procedure to get this answer
- all we needed to do is start at the right and bunch the digits into groups of 2
- we wanted groups of 2 because 100 = 102
- likewise, groups of three would convert to base 1000
- whenever one base is a power of the other, we can convert just by grouping like this
- and we don't have to do any arithmetic
- this is going to be really handy

