This time we have two vertical red lines dividing our addresses into chunks
This elaborates the pattern that we got in the previous page
The horizontal lines separate these chunks
Now look at the middle column; in any chunk, all of the rows have the same value
These also count: 0, 1, 2, 3 and form bigger chunks that are separated by the blue lines
Sure enough, the left column has the same value throughout each of these larger chunks

Long Division

Let's pick a nice random number; how about 12345?
Let's divide it by 100; the quotient is 123 and the remainder is 45. I hope that's not a shock.
Now let's divide it by 1000; the quotient is 12 and the remainder is 345. I hope you see a pattern forming.
We can divide by a power of 10 and get the quotient and remainder without doing any real work
1. take the exponent
2. count that many places from the right end and draw a line
100 is 10², so we count 2 places from the right and get 123-45, which is the right answer.
1000 is 10³, so we count 3 places from the right and get 12-345, which is the right answer.
We can do the same thing in binary notation when dividing by powers of 2.
That is, to divide 1011001000101101 by 32, we count in 5 places from the right: 10110010001-01101
The hardware exploits this, particularly in cache memories.
They just run wires from the remainder part to where they need to go and wires from the quotient part to where they need to go.
That's all there is to it. Nothing needs to be done while the CPU is running. Things just go where they need to be.

Offsets

To get started, let's look at the bytes in a word.
There are 4 of them.
Their offsets are 0, 1, 2, and 3.
In each case, a byte's offset is the distance between that byte and the byte at the beginning of the word.
Here is a picture of the word at address 0x10 divided into bytes.

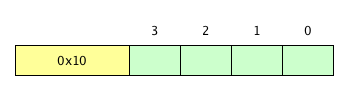
Their addresses are 0x10, 0x11, 0x12, and 0x13.
In binary that is 1-0000, 1-0001, 1-0010, and 1-0011
The first three bits are the same in all four addresses: 100 (fun with address spaces).
The last two bits hold the offsets: 00, 01, 10, 11.
The address of the word is the same as the address if its first byte: 0x1-0000.
We can calculate the offset of any byte by subtracting the word's address from the byte's address.
Turning that around, we can calculate the address of any byte by adding its offset to the address of the word that it is a part of.

Think of the table as holding the addresses of 64 consecutive bytes.
The two vertical red lines divide the addresses into three parts.
The two bits on the left are what we'll call block numbers.
There are four blocks: 0, 1, 2, and 3.
The four bits on the left are what we called word numbers on the cache page.
You get a word number by dividing the word's address by 4, or equivalently, by dropping the 2 bits at its right end.
There are 16 of these: 0 - 15.
The two bits in the middle are the word's offset in its block.
The two bits on the right are a byte offset, as we've just discussed.
If we divide an address by 4, the quotient is the word number, and the remainder is the byte offset.
If we divide a word number by 4, the quotient is the block number, and the remainder is the word's offset in its block.
Here's a 6-bit address divided into its 3 pieces as we've just done:

When we do caches, these red lines can move:
- modern CPUs have 64-bit words, i.e. there are 8 bytes in a word, so the byte offset is 3 bits on these machines
- typical caches these days have 64 bytes in a block, which is 8 64-bit words, so that offset would be 3 bits as well