Constructing Masks

If you need to set bits, use or

If you need to clear bits, use and

If you need to set some bits and clear others, use one of each

• Each of our operators (and/or) has what we will call a dominant value.
• That is a value that, when composed with another value, yields itself.
  • For or's the dominant value is 1 because (1 or x) = 1 for any x.
  • For and's the dominant value is 0 because (0 and x) = 0 for any x.
• Each of our operators (and/or) has what we will call a recessive value.
• That is a value that, when composed with another value, yields the other value.
  • For or's the recessive value is 0 because (0 or x) = x for any x.
  • For and's the recessive value is 1 because (1 and x) = x for any x.
• You can use truth tables to verify all of this.

Here is a diagram showing a 32-bit value in $t0 with asterisks in the bits we need to set or clear: 2, 9, 13, 21

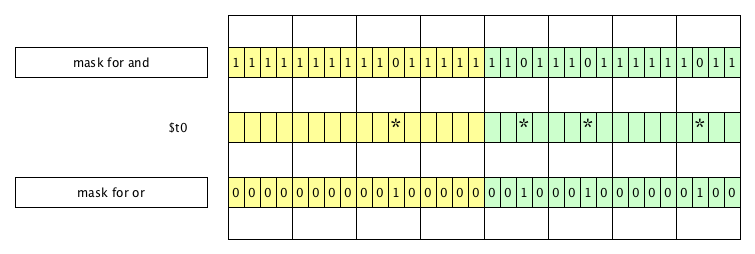
It also shows the binary masks we would need to do the setting or clearing

The general rule is to use dominant values against the bits we need to set or clear and recessive values against the bits we need to leave as they are

This general rule has two special cases: one for setting bits, and one for clearing bits

• For bits we need to set, we use or; the mask will have dominant 1's where we need to set bits and recessive 0's everywhere else.
• For bits we need to clear, we use and; the mask will have dominant 0's where we need to clear bits and recessive 1's everywhere else.

• The diagram also has boxes that divide the bits into groups of 4.
• That helps us look at the diagram and read the masks in hexadecimal.

We need to be careful about the size of the mask

• If all the bits to be changed are in the green half of $t0 (i.e. if there were no * in bit 21), we can use a 16-bit mask.
• In this case, the mask would be 0xDDFB for and; it would be 0x2204 for or.
• So we would write one of the following:
  • andi $t0 $t0 0xDDFB
  • ori $t0 $t0 0x2204
• If there are bits to be changed in the yellow half (i.e. as the diagram is), then we need a 32-bit mask.
• In this case, the mask would be 0xFFDFDDFB for and; it would be 0x00202204 for or.
• So we would write them this way:
  • andi $t0 $t0 0xFFDFDDFB
  • ori $t0 $t0 0x00202204
• But MARS would assemble them this way, which might be a surprise at first:
  • lui $at 0xFFDF
  • ori $at $at 0xDDFB
  • and $t0 $t0 $at
  • - - - - - - - - - - - - - - - - - -
  • lui $at 0x0020
  • ori $at $at 0x2204
  • or $t0 $t0 $at
• The first two instructions copy our entire 32-bit mask into $at.
• Then $at becomes the mask, and the R-format version of our and/or is used against it to do the right thing.

Summary

• Decide whether to use and or or.
• Decide whether to use a 16-bit mask or a 32-bit mask.
• Write the dominant value next to the bits to be set or cleared.
• Write the recessive value next to the bits to be left as they are.
• This gives you the mask in binary.
• Convert the binary to hexadecimal for use in MIPS source code.