Converting decimal to another base

This is a completely different algorithm that involves dividing by the new base a number of times.

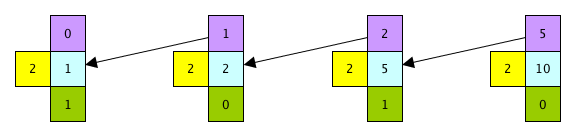
Let's convert 10 decimal to binary; we already know that the answer should be 1010.

• start at the right side of the page
• divisor (always 2 in this case) is yellow; dividend is aqua; quotient is purple; remainder is green
• divide the original numeral (10) by the new base (2), which gives you a quotient (5) and a remainder (0)
• long division procedure guarantees that the remainder will be less than the divisor (2 in this case)
• now repeat until the quotient is zero
  • move over to the left a bit
  • write down the quotient from the last division (arrows)
  • make it a new division problem using the same divisor
  • do the division, getting another quotient and remainder
• the answer is the string of remainders read left to right (1010 in this case)