Converting binary to decimal

Representing numbers with binary numerals follows the same rules as representing them with decimal numerals.

• a number is represented as a string of digits
• each digit is at least 0 and less than the base
• we can calculate the value by multiplying each digit by the appropriate power of the base:
  • the exponents for these powers begin at zero at the right end
  • they increase by one each time we take a step to the left
• adding all these products gives us the value of the number our numeral represents

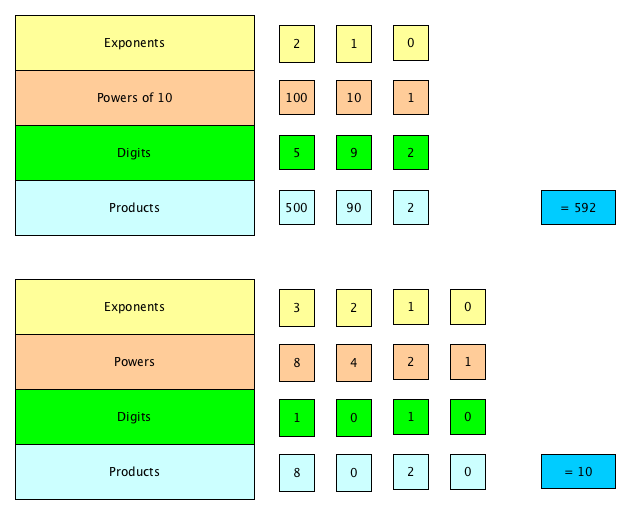
As an example, let's do this for 592 base ten.

• our string of digits is 592 (third line)
• each digit is at least 0 and less than 10
• we can calculate the value by multiplying each digit by the appropriate power of 10:
  • the exponents, from right to left, are 0, 1, 2 (top line)
  • the powers, from right to left, are 1, 10, 100 (second line)
  • the products (multiply second line by third line) are then 2, 90, 500 (bottom line)
• adding all these products gives us 592 (converting base 10 to base 10 gives us the numeral we started with; duh)

Now let's do 1010 base two.

• our string of digits is 1010 (third line)
• each digit is at least 0 and less than 2
• we can calculate the value by multiplying each digit by the appropriate power of 2:
  • the exponents, from right to left, are 0, 1, 2, 3 (top line)
  • the powers, from right to left, are 1, 2, 4, 8 (second line)
  • the products (multiply second line by third line) are then 0, 2, 0, 8 (bottom line)
• adding all these products gives us 10